# 后缀自动机 (Suffix automata, SAM)

参考资料 :

KesdiaelKen 的博客

OI-WiKi 后缀自动机 (SAM)

此篇博客中的大部分图转自 KesdiaelKen 的博客，如有侵权，请联系删除

(此篇博客的示例字符串为 aababa )
( $fa$ 边在其他博客或许被称作后缀 link（后缀链接）)

# 概述

后缀自动机 (Suffix Sutomaton, SAM) 是一个能解决许多字符串相关问题的有力的数据结构 .
一个字符串的 SAM 是一个接受原字符串的所有后缀的最小 DFA (确定性有限自动机或确定性有限状态自动机) .
SAM 可以在线性时间内解决 " 一个字符串中另一个字符串的所有的出现位置 "和" 字符串中不同子串计数 " 的问题 .
SAM 将子串信息高度压缩储存，其时空复杂度均为 $O(n)$ .

# 性质

SAM 是一张有向无环图 (DAG) .
SAM 有一个源点，若干个终止点 . SAM 的边表示在当前字符串后加上该边代表的字母 .
在 SAM 中，从源点到任意节点均能构成一个字符串，且该字符串一定为原串的子串 .
在 SAM 中，从源点到任意终止节点构成的字符串均为原串的后缀 .
在 SAM 中，从源点出发的任意两条 不同路径 所构成的字符串不同 .

# endpos

# 定义

对于字符串 $s$ 的一个子串 $t$ , 在 $s$ 中所有出现位置的末尾标号所组成的集合，我们称之为 $endpos(t)$ .

# 性质及推论

如果两个子串的 $endpos$ 相同，则其中一个必定是另一个的后缀 .
对于任意两个子串 $t_1$ 和 $t_2$ $(len_{t_{1}} \le len_{t_{2}})$ , 要么 $endpos(t_2) \subset endpos(t_1)$ , 要么 $endpos(t_1) \cap endpos(t_2) = \empty$ .
对于 $endpos$ 相同的子串，将其归为一个 $endpos$ 等价类，本文中部分将简称 “类” . 对于任意一个 $endpos$ 等价类，其包含的所有字符长度从大到小是连续，且较短的子串为较长子串的后缀 .
$endpos$ 等价类的个数为 $O(n)$ 级别的，最终的集合个数不会超过 $2n$ 个 .

对于一个类 $A_0$ , 其中最长子串记为 $t_0$ , 在其前面加上一字符形成的字串 (属于原串的子串) $t_1$ , 必定不属于该类，而 $t_1$ 所在类 $A_1$ 必定是 $A_0$ 的子集，即 $A_1 \subset A_0$ .

对于一个类 $A_0$ , 其中最长子串记为 $t_0$ , 在其加上两个不同的字符形成的字串 (属于原串的子串) $t_1$ 和 $t_2$ , $t_1$ 与 $t_2$ 所在类 $A_1$ 和 $A_2$ , 必然满足 $A_1 \cap A_2 = \empty$ . 这可以看做类 $A_1$ 和 $A_2$ 由类 $A_0$ 分裂出来 .

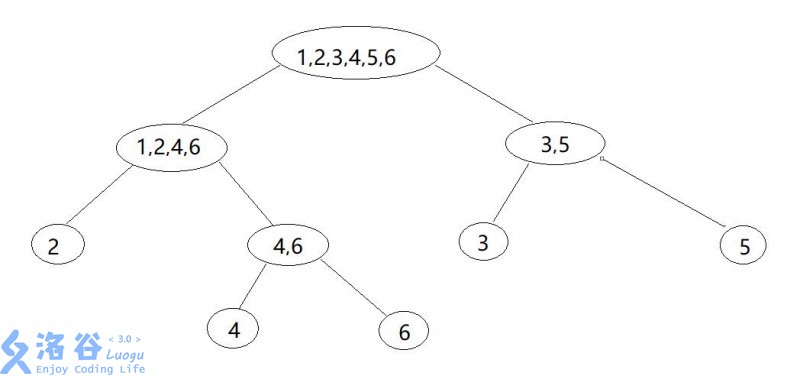
由前两条可以得出，某一字符串所有子串所形成的各个 $endpos$ 等价类满足类似如下图的父子关系 (树形结构， $parent \; tree$ ) , 其节点个数为 $O(n)$ 级别，叶节点最多有 $n$ 个，因此节点总数最多有 $2n - 1$ 个，当且仅当其按类似于线段树方法的分割时，满足上界 .

一个 $endpos$ 等价类 $A$ 中，最长子串的长度记为 $len(A)$ , 最短子串的长度记为 $minlen(A)$ . 我们定义 $fa(A)$ 为 $endpos$ 等价类 $A$ 在 $parent \; tree$ 上的父亲，则有 $len(fa(A)) + 1 = minlen(A)$

在 $parent \; tree$ 中，我们只需要记录该节点 (类) 的 $len$ 即可，因为 $minlen$ 可以由其父节点推出 .

在此，我们定义 $longest(A)$ 为 $endpos$ 等价类 $A$ 中的最长串， $shortest(A)$ 为该类中的最短串 .

此时，我们发现这棵 $parent \; tree$ 的节点就是我们要寻找的 SAM 上的节点，只是连边不一样罢了 .
其空串所在节点为 SAM 的源点 ( root ) . 终止节点即为最大子串，也就是整个原串所在的节点，和其各个祖先节点。而这些终止节点在 SAM 上代表着原串的所有后缀 .
我们试着在上面那棵 $parent \; tree$ 上构建 SAM , 会出现一棵 极具魅力 的树形结构 :
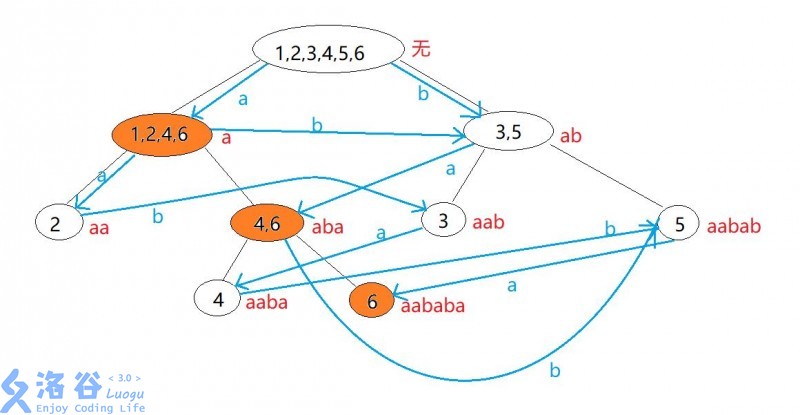
摘自KesdiaelKen的博客
在这张图上，沿着 $parent \; tree$ 上的边走指在字符串前面加字符形成新子串，沿着 SAM 中的边 (蓝色且带有箭头的边) 走指在字符串后面加字符形成新子串。由此特性， $parent \; tree$ 主要用来求各字符串的性质，而 SAM 主要用来直接跑字符串 .

SAM 的边是 $O(n)$ 级别的

对于一个 SAM : 选出其任意一棵生成树，在各个终止节点往源点跑属于该类的各个子串 (其实就是跑后缀) . 对于跑的方式嘛... 按照原自动机唯一能到达此串的边往回跑，并非指考虑边所代表的字符 .
我们在终止节点按照一定顺序跑后缀，如果能返回源点，则跑下一个子串。每加一个边必定会多一个没有跑过的后缀，增加的边不会超过后缀个数，所以数量级为 $O(n)$ .

# SAM 的构造

	#include<bits/stdc++.h>
	using namespace std;
	const int MAXN = 1e5+10;
	struct node
	{
	int next[26];
	int len,fa;
	}tr[MAXN<<1];
	int lst=1,tot=1;
	void add(int c)
	{
	int p = lst, np = lst = ++tot;
	tr[np].len = tr[p].len+1;
	for( ; p and tr[p].next[c] == 0; p = tr[p].fa)
	tr[p].next[c] = np;
	if(!p) tr[np].fa = 1;
	else
	{
	int q = tr[p].next[c];
	if(tr[q].len == tr[p].len+1) tr[np].fa = q;
	else
	{
	int nq = ++tot;
	tr[nq] = tr[q];
	tr[nq].len = tr[p].len+1;
	tr[q].fa = tr[np].fa = nq;
	for( ; p and tr[p].next[c] == q; p = tr[p].fa)
	tr[p].next[c] = nq;
	}
	}
	}
	int len; char s[MAXN];
	int main()
	{
	scanf("%s",s+1); len = strlen(s+1);
	for(int i = 1; i <= len; i += 1) add(s[i]-'a');
	return 0;
	}

# Part.1

	struct node
	{
	int next[26];
	int len,fa;
	}tr[MAXN<<1];

$next[26]$ 即为 SAM 上的连边， $fa$ 指向的是 $parent \; tree$ 上的父亲节点， $len$ 代表的是当前节点所代表的 $endpos$ 等价类中所包含的子串的最长长度 .

# Part.2

	int p = lst, np = las = ++tot;
	tr[np].len = tr[p].len+1;
	for( ; p and tr[p].next[c] == 0; p = tr[p].fa)
	tr[p].next[c] = np;

将字符串拆成若干个单个字符，依次插入 SAM 中，记当前插入的字符为 $c$ , 其在全串中的下标为 $n$ .
记插入前的字符串为旧串，插入后的字符串为新串 .
$lst$ 指的节点代表旧串中的最长前缀 (即旧串本身) , $np$ 指的节点是新串的最长前缀 (即新串本身) .

显然，新串长度为旧串加一 .

$p$ 为终止节点，为旧串后缀，其 $parent \; tree$ 上的所有祖先也均为后缀，而新加入字符后 $endpos$ 改变的只有旧串后缀 (加上新加的字符变为新串后缀， $endpos$ 中会多个 $n$ ) , 所以我们只需跳 $p$ 的 $fa$ 去遍历所有后缀即可 .

若 $p$ 没有 $c$ 的出边，则代表 $p$ 串加上字符 $c$ 组成的子串在旧串中没有出现过，所以其 $endpos$ 中有且仅有 $n$ , 与节点 $np$ 相同，所以直接将 $p$ 的 $c$ 字符出边连向 $np$ 即可 .

到遇到第一个有 $c$ 出边的后缀 $p$ 时，停止循环。至于这时跳出为什么嘛... 当前的 $p$ 有 $c$ 的出边时，代表着旧串中出现过 $p$ 串加 $c$ 组成的子串，此时 $endpos$ 与 $np$ 不一样 ( $p$ 的所有祖先也一样 ) , 此时跳出循环即可 .

# Part.3

if(!p) tr[np].fa = 1;

若找完所有后缀，也没能找到一个有 $c$ 出边的后缀，这说明新的后缀是新的（之前从未有过的），之前的所有字串都不可能成为这个新串的后缀，所以 $fa$ 直接连到根就好。

# Part.4

	int q = tr[p].next[c];
	if(tr[q].len == tr[p].len+1) tr[np].fa = q;

$p$ 是我当前找到的原串后缀的一类字串中有 $c$ 出边的一个 (最先跳到的)， $q$ 是 $p$ 加上 $c$ 构成的字串，如果他们两个长度连续，表示 $q$ 所在等价类都是新串后缀，连 $fa$ 边即可。

# Part.5

	else
	{
	int nq = ++tot;
	tr[nq] = tr[q];
	tr[nq].len = tr[p].len+1;
	tr[q].fa = tr[np].fa = nq;
	for( ; p and tr[p].next[c] == q; p = tr[p].fa)
	tr[p].next[c] = nq;
	}

如果长度不连续，那么新串的后缀只是其中一部分，我们把这一部分分离出来， $next$ 边继承原来的即可，按照字串的后缀关系连一下 $fa$ 边，再把所以原串后缀有 $c$ 出边的 $c$ 出边更新连到新分离出来的这个点，这样就构建完了。

字符串